ajout cours parcours, POO sur les graphes
This commit is contained in:
@@ -39,6 +39,16 @@ def bfs(graphe, depart):
|
|||||||
file.append(voisin)
|
file.append(voisin)
|
||||||
```
|
```
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
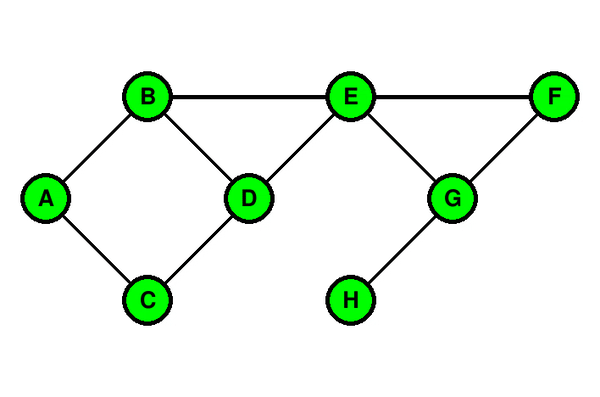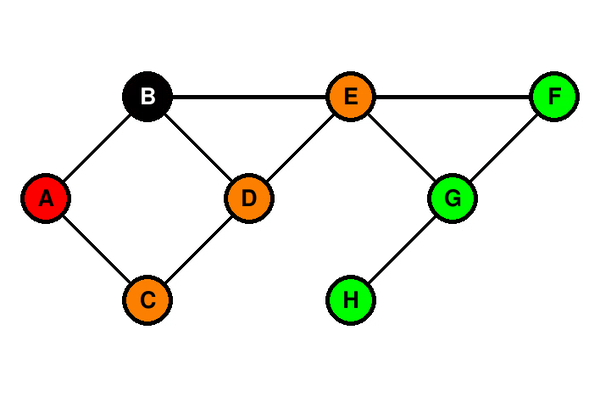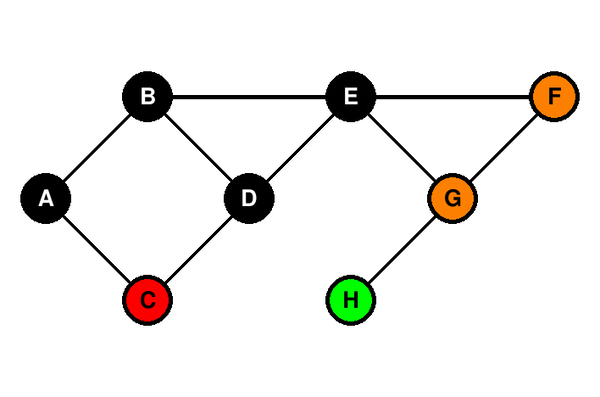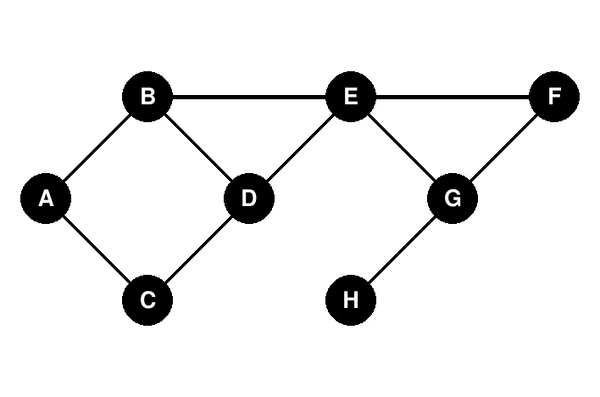
### Illustration du parcours en largeur
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
### Parcours en profondeur (DFS - Depth First Search)
|
### Parcours en profondeur (DFS - Depth First Search)
|
||||||
|
|
||||||
Le parcours en profondeur explore un chemin le plus loin possible avant de revenir en arrière. C’est une approche de type pile (LIFO).
|
Le parcours en profondeur explore un chemin le plus loin possible avant de revenir en arrière. C’est une approche de type pile (LIFO).
|
||||||
@@ -64,6 +74,14 @@ def dfs(graphe, depart, visite=None):
|
|||||||
dfs(graphe, voisin, visite)
|
dfs(graphe, voisin, visite)
|
||||||
```
|
```
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
### Illustration
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
|
----------
|
||||||
|
|
||||||
### Détection de cycles dans un graphe
|
### Détection de cycles dans un graphe
|
||||||
|
|
||||||
Un cycle est une chaîne fermée sans répétition d’arêtes. Pour détecter un cycle dans un graphe non orienté, on peut utiliser DFS :
|
Un cycle est une chaîne fermée sans répétition d’arêtes. Pour détecter un cycle dans un graphe non orienté, on peut utiliser DFS :
|
||||||
@@ -138,3 +156,12 @@ class Graphe:
|
|||||||
print(f"{sommet}: {', '.join(map(str, voisins))}")
|
print(f"{sommet}: {', '.join(map(str, voisins))}")
|
||||||
```
|
```
|
||||||
|
|
||||||
|
------
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
Auteur : Florian Mathieu
|
||||||
|
|
||||||
|
Licence CC BY NC
|
||||||
|
|
||||||
|
<a rel="license" href="http://creativecommons.org/licenses/by-nc-sa/4.0/"><img alt="Licence Creative Commons" style="border-width:0" src="https://i.creativecommons.org/l/by-nc-sa/4.0/88x31.png" /></a> <br />Ce cours est mis à disposition selon les termes de la <a rel="license" href="http://creativecommons.org/licenses/by-nc-sa/4.0/">Licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International</a>.
|
||||||
|
|||||||
70
Graphes/POO.md
Normal file
70
Graphes/POO.md
Normal file
@@ -0,0 +1,70 @@
|
|||||||
|
## Graphes et POO
|
||||||
|
|
||||||
|
> Tout comme les arbres, il nous est possible de représenter les graphes sous la forme d'une classe Python.
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
Nous souhaitons représenter le graphe ci-dessous sous la forme d'une classe Graphe.
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
|
On pourra créer celui-ci de cette manière
|
||||||
|
|
||||||
|
```python
|
||||||
|
g = Graphe(['A', 'B', 'C', 'D', 'E'])
|
||||||
|
g.ajoute_arete('A', 'B')
|
||||||
|
g.ajoute_arete('A', 'C')
|
||||||
|
g.ajoute_arete('A', 'D')
|
||||||
|
g.ajoute_arete('A', 'E')
|
||||||
|
g.ajoute_arete('B', 'C')
|
||||||
|
g.ajoute_arete('C', 'D')
|
||||||
|
g.ajoute_arete('D', 'E')
|
||||||
|
```
|
||||||
|
|
||||||
|
Nous souhaitons aussi pouvoir tester si deux sommets sont voisins avec la méthode `sont_voisins` :
|
||||||
|
|
||||||
|
```python
|
||||||
|
>>> g.sont_voisins('E', 'A')
|
||||||
|
True
|
||||||
|
>>> g.sont_voisins('E', 'B')
|
||||||
|
False
|
||||||
|
```
|
||||||
|
|
||||||
|
Enfin, nous voulons pouvoir obtenir facilement la liste de tous les voisins d'un sommet avec la méthode `voisins`:
|
||||||
|
|
||||||
|
```python
|
||||||
|
>>> g.voisins('C')
|
||||||
|
['A', 'B', 'D']
|
||||||
|
```
|
||||||
|
|
||||||
|
L'objet de type `Graphe` aura comme attributs :
|
||||||
|
|
||||||
|
- une liste `liste_sommets` (donnée en paramètre dans la liste `liste_sommets`)
|
||||||
|
- un dictionnaire `adjacents`, où chaque sommet se verra attribuer une liste vide `[]`.
|
||||||
|
|
||||||
|
### Implémentation
|
||||||
|
|
||||||
|
```python
|
||||||
|
class Graphe:
|
||||||
|
def __init__(self, liste_sommets):
|
||||||
|
self.liste_sommets = liste_sommets
|
||||||
|
self.adjacents = {sommet : [] for sommet in liste_sommets}
|
||||||
|
|
||||||
|
def ajoute_arete(self, sommetA, sommetB):
|
||||||
|
self.adjacents[sommetA].append(sommetB)
|
||||||
|
self.adjacents[sommetB].append(sommetA)
|
||||||
|
|
||||||
|
def voisins(self, sommet):
|
||||||
|
return self.adjacents[sommet]
|
||||||
|
|
||||||
|
def sont_voisins(self, sommetA, sommetB):
|
||||||
|
return sommetB in self.adjacents[sommetA]
|
||||||
|
```
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
-------------
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
Merci à [Gilles Lassus](https://glassus.github.io/terminale_nsi/T1_Structures_de_donnees/1.4_Graphes/cours/#3-creation-dune-classe-graphe) pour la source.
|
||||||
BIN
Graphes/assets/graphe_poo.png
Normal file
BIN
Graphes/assets/graphe_poo.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 11 KiB |
Reference in New Issue
Block a user