## Parcours de graphes
> Avoir une représentation de données, c'est bien.
> Pouvoir parcourir ces données de manière rapide et simple, c'est mieux.
### Le programme
------
### Parcours en largeur (BFS - Breadth First Search)
Le parcours en largeur d’un graphe consiste à explorer tous les voisins d’un sommet avant de passer aux voisins de ces voisins. C’est une approche de type file (FIFO).
#### Algorithme BFS :
1. Choisir un sommet de départ et l’ajouter à une file d’attente.
2. Marquer ce sommet comme visité.
3. Tant que la file n’est pas vide :
- Retirer le sommet en tête de la file.
- Ajouter tous ses voisins non encore visités dans la file et les marquer comme visités.
#### Implémentation en Python :
```python
from collections import deque
def bfs(graphe, depart):
visite = set()
file = deque([depart])
visite.add(depart)
while file:
sommet = file.popleft()
print(sommet, end=" ")
for voisin in graphe.get(sommet, []):
if voisin not in visite:
visite.add(voisin)
file.append(voisin)
```
### Illustration du parcours en largeur
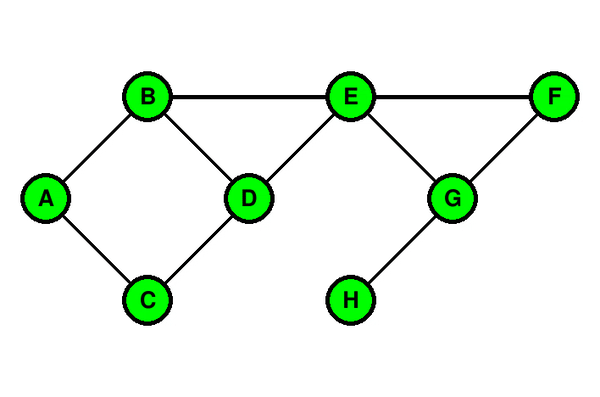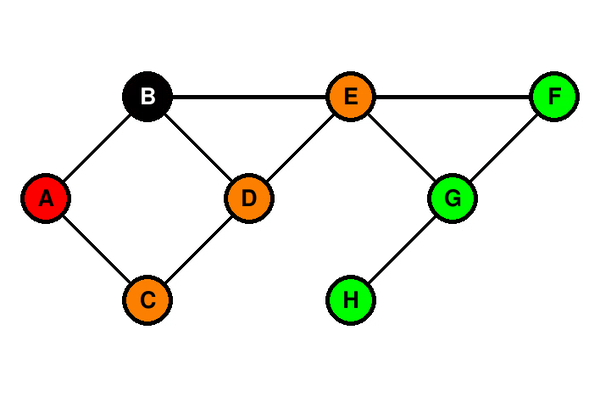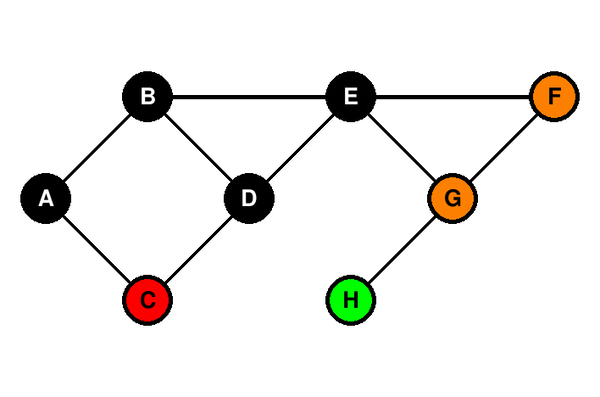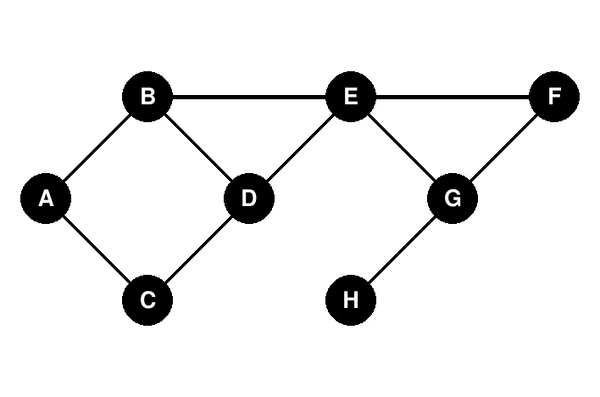
### Parcours en profondeur (DFS - Depth First Search)
Le parcours en profondeur explore un chemin le plus loin possible avant de revenir en arrière. C’est une approche de type pile (LIFO).
#### Algorithme DFS :
1. Choisir un sommet de départ et l’empiler.
2. Marquer ce sommet comme visité.
3. Tant que la pile n’est pas vide :
- Retirer le sommet du sommet de la pile.
- Ajouter tous ses voisins non encore visités dans la pile et les marquer comme visités.
#### Implémentation en Python :
```python
def dfs(graphe, depart, visite=None):
if visite is None:
visite = set()
visite.add(depart)
print(depart, end=" ")
for voisin in graphe.get(depart, []):
if voisin not in visite:
dfs(graphe, voisin, visite)
```
### Illustration
----------
### Détection de cycles dans un graphe
Un cycle est une chaîne fermée sans répétition d’arêtes. Pour détecter un cycle dans un graphe non orienté, on peut utiliser DFS :
#### Implémentation en Python :
```python
def a_un_cycle(graphe, sommet, visite, parent):
visite.add(sommet)
for voisin in graphe.get(sommet, []):
if voisin not in visite:
if a_un_cycle(graphe, voisin, visite, sommet):
return True
elif parent != voisin:
return True
return False
```
### Recherche d’un chemin dans un graphe
On peut utiliser DFS pour rechercher un chemin entre deux sommets.
#### Implémentation en Python :
```python
def trouver_chemin(graphe, depart, cible, chemin=None):
if chemin is None:
chemin = []
chemin.append(depart)
if depart == cible:
return chemin
for voisin in graphe.get(depart, []):
if voisin not in chemin:
nouveau_chemin = trouver_chemin(graphe, voisin, cible, chemin.copy())
if nouveau_chemin:
return nouveau_chemin
return None
```
### Applications des algorithmes de graphes
#### 1. Parcours d’un labyrinthe
Un labyrinthe peut être modélisé sous forme de graphe où chaque case est un sommet et chaque passage est une arête. BFS est souvent utilisé pour trouver le chemin le plus court vers la sortie.
#### 2. Routage dans Internet
Internet est un graphe où les routeurs sont des sommets et les connexions entre eux sont des arêtes. Des algorithmes comme Dijkstra ou Bellman-Ford (que l'on verra prochainement ) permettent de trouver le chemin optimal entre deux nœuds.
### Illustrer l’utilisation des classes
On peut modéliser un graphe en POO avec une classe `Graphe` :
```python
class Graphe:
def __init__(self):
self.adjacence = {}
def ajouter_sommet(self, sommet):
if sommet not in self.adjacence:
self.adjacence[sommet] = []
def ajouter_arete(self, sommet1, sommet2):
self.ajouter_sommet(sommet1)
self.ajouter_sommet(sommet2)
self.adjacence[sommet1].append(sommet2)
self.adjacence[sommet2].append(sommet1)
def afficher(self):
for sommet, voisins in self.adjacence.items():
print(f"{sommet}: {', '.join(map(str, voisins))}")
```
------
Auteur : Florian Mathieu
Licence CC BY NC
Ce cours est mis à disposition selon les termes de la Licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International.